⇚ Inicio
somerby.net/mack/logic
Introducción
Esta aplicación web (en lo sucesivo denominada "el software" o "la aplicación") decide la validez / satisfacibilidad / inconsistencia de ciertos tipos de expresiones de la lógica simbólica.
El software, en su parte principal, está escrito en C# y traducido a JavaScript con Saltarelle. El código fuente se encuentra en GitHub. Se utiliza Viz.js para generar los diagramas. La función que hace tablas de verdad está adaptada del código escrito por Michael Rieppel.
Agradezco a Maximiliano Paesani su ayuda en la traducción de la aplicación web al español.
Instrucciones
Para usar esta aplicación, escriba una expresión lógica en el cuadro de texto de la página principal. Luego haga clic en el botón "Decidir". Si la expresión es decidible en la aplicación, se mostrará el resultado. De lo contrario, mostrará algún tipo de mensaje explicando cuál es el error. La sección 'El lenguaje' especifica cómo escribir expresiones lógicas para la aplicación. Si está buscando ejemplos de expresiones, haga clic en cualquiera de los botones bajo el encabezado titulado "Ejemplos", y la aplicación llenará el cuadro de texto con alguna expresión a decidir.
Si hace clic en el botón "Diagramar", la aplicación mostrará un diagrama que explicita cómo la aplicación interpreta la expresión escrita en el cuadro de texto. El diagrama es una representación gráfica de la estructura de datos que la aplicación está usando efectivamente para decidir la expresión.
Si en el cuadro de texto hay una expresión sintácticamente válida perteneciente a la lógica proposicional, se habilitará el botón "Tabla de verdad". Al hacer clic allí, la aplicación generará la tabla de verdad correspondiente.
Al hacer clic en el botón "Ejemplo", la aplicación intentará encontrar un tipo de mundo en el que la expresión sea verdadera. Si tiene éxito, mostrará una descripción de ese tipo de mundo.
El botón "Contraejemplo", inicia la búsqueda de un tipo de mundo que haga falsa la expresión, y si lo encuentra m su descripción.
El botón "árbol semántico" redirigirá la expresión al generador de árboles semánticos(Tree Proof Generator) de wo. Es una aplicación web que usa tablas semánticas (árboles) para verificar la validez de una expresión, y proporciona una prueba si decide que es válida. El botón "árbol semántico" se habilitará siempre que haya una expresión sintácticamente válida en el cuadro de texto que no contenga identificaciones u operadores modales. Si desea evaluar una expresión que contiene predicados binarios (relaciones), use el Generador de árboles semánticos.
El lenguaje
Elementos del lenguaje
El lenguaje tiene estos elementos:
- Operadores lógicos unarios y binarios
- Variables
- Constantes Individuales
- Predicados sobre una variable y predicados sobre cero variables (proposiciones)
- Predicados sobre dos variables (relaciones)
- Agrupación mediante paréntesis
- Generalizaciones universales, cuantificaciones existenciales y y descripciones definidas
- Identidad
- Los operadores modales de necesidad y posibilidad
- Proposiciones de dos términos
- Algunas afirmaciones simples sobre números
- Reemplazos de texto
- Un símbolo de "por lo tanto"
Operadores lógicos
Los operadores lógicos que el software reconoce son:
| Operador | Símbolo | Descripción |
|---|---|---|
| negación | ~ | "no" lógico |
| conjunción | & | "y" lógico |
| disyunción | | | "o" lógico |
| condicional material | -> | Si … entonces … |
| bicondicional | <=> | Equivalencia lógica |
| negación conjunta | ! | "nor" lógico |
| disyunción excluyente | ^ | "Xor" lógico |
| implicación estricta | -< | necesariamente si … entonces … |
Todos los operadores lógicos binarios son asociativos por la izquierda y tienen las siguientes precedencias:
| Precedencia | Operadores |
|---|---|
| superior | &, ! |
| … | | |
| … | ->, -< |
| inferior | <=>, ^ |
Por ejemplo,
A|B&C->D
se interpreta como significando lo mismo que
(A|(B&C))->D
La negación es asociativa por derecha y precede a cualquier operador binario, por ello
~P & ~Q
se interpreta como significando lo mismo que
(~P) & (~Q)
Variables
Las variables son letras minúsculas únicas que representan algún objeto. Cada variable está ligada por un cuantificador. Cualquier letra minúscula que no esté ligada por un cuantificador se interpretará como una constante individual.
Constantes individuales
Las constantes individuales, como las variables, son letras minúsculas únicas. Representan algún objeto fijo. Cualquier letra minúscula que no esté limitada por un cuantificador se interpretará como una constante individual. Creo que las constantes no son completamente necesarias en la lógica simbólica. El siguiente argumento:
Hx->Mx // Todo hombre es mortal. Hs // Socrates es hombre. -> // Por lo tanto Ms // Socrates es mortal.
podría también representarse sin constantes individuales como
Hx->Mx // Todo hombre es mortal. (3x,Sx) & ([]x,Sx->y,Sy->x=y) & x,Sx->Hx // Socrates es hombre. -> // Por lo tanto x,Sx->Mx // Socrates es mortal.
lo cual, aunque más complicado, es en cierto modo mejor, porque hace explícito lo que típicamente suponemos acerca de Sócrates: que existió y que era, por definición, un individuo único. Aun así, creo que las constantes individuales son una característica demasiado útil para excluirlas del software. El uso de una constante individual implica que el objeto denotado por ella realmente existe. Esta no es la única forma de interpretar constantes individuales, pero es la más fácil de implementar en este software. Debido a esta interpretación, el software decidirá que 3x,x=g es necesariamente cierto. Los objetos posibles (aquellos que pueden o no existir) y los objetos imposibles (los que nunca podrían existir) se pueden representar con predicados unarios.
Como todavía no he encontrado una manera satisfactoria de decidir expresiones que contienen tanto operadores modales como constantes individuales, el software rechaza cualquier expresión de este tipo.
Predicados sobre cero variables
Un predicado de cero variables, que se puede considerar como una proposición verdadero/falso, se representa con una sola letra.
Predicados en una variable
Una predicación sobre una variable, que puede considerarse como la afirmación de que un objeto tiene alguna propiedad, se representa con una sola letra mayúscula (el predicado) seguida de una sola letra minúscula (la variable). Se puede usar la misma letra mayúscula como predicado sobre una variable y como predicado sobre cero variables en la misma expresión y el software las tratará como predicados distintos, por ejemplo
x,Fx->F
será interpretado de la misma manera que
x,Fx->P
porque la primera "F" se interpreta como un predicado unario y la segunda "F" se interpreta como un predicado nulo.
Predicados en dos variables
Una predicación sobre dos variables, que puede considerarse como la afirmación de que dos objetos tienen alguna relación entre sí, se representa con una sola letra mayúscula (el predicado) seguida de dos letras minúsculas (las variables). El algoritmo de decisión no admite predicados sobre dos variables y, por lo general, rechazará una expresión que las contenga. Sin embargo, las expresiones que tienen predicados en dos variables pueden evaluarse con el Generador de árboles semánticos, si no contienen también operadores modales o identificaciones.
Agrupación
Las expresiones se pueden agrupar con paréntesis. Funcionan igual que los paréntesis en álgebra o en otras lógicas simbólicas.
Generalizaciones universales
Una generalización universal es una variable seguida de una coma y seguida de la expresión a la que se aplica la generalización. De acuerdo con esto, se podría escribir
x,Ax
para decir "todo es asombroso". La generalización liga toda la expresión que sigue a la coma, hasta un paréntesis de cierre o el final de la línea de texto en la que se encuentra la generalización. Así
x,Fx & y,Jy
generaliza sobre la sub-expresión
Fx & y,Jy
en vez de ser sólo una generalización sobre Fx. Se recomienda añadir paréntesis a los fines de mayor claridad. Por ejemplo:
(x, Fx & (y,Jy))
Una variable siempre está ligada a la generalización delimitante más próxima, por ello en
x, (x,F->Px) & Jx
la x en Px está ligada por la segunda generalización universal y la x en Jx está ligada por la primera.
Cuantificación existencial
Una cuantificación existencial es un símbolo "3" seguido de una variable, seguida de una coma y, finalmente, seguida de una expresión a la cual se aplica la cuantificación. Por ejemplo,
3x, Fx & Bx
podría significar "Hay una fuente llena de sangre". Las mismas reglas de aplicabilidad y ligación de variables definidas para las generalizaciones universales se aplican también a las cuantificaciones existenciales.
Descripciones definidas
Una descripción definida es un "1" seguido de una variable, seguida de una coma, seguida de una expresión que, se supone, describe exactamente un objeto. Por ejemplo,
1x,Rx
podría significar "existe sólo un Roy Orbison".
Identidad
Una identidad entre dos objetos consiste en una letra minúscula seguida de un signo igual seguido de otra letra minúscula, por ejemplo
x,y, (Fx & x=y) -> Fy
es una afirmación donde "x=y" significa x es el mismo objeto que y.
Operadores modales
El software reconoce dos operadores modales, "[]" para necesidad y "<>" para posibilidad. Son asociativos por la derecha y tienen la misma precedencia que la negación. El tipo de modalidad representada por estos operadores es la modalidad alética.
Proposiciones de dos términos
El software reconoce proposiciones de dos términos en lo que se suele denominarse lógica "de términos", "aristotélica" o "tradicional". Trata las proposiciones de dos términos como enunciados abreviados de la lógica de predicados unarios. Son una letra mayúscula que representa el término del sujeto, seguida de una letra minúscula que representa la forma de la proposición, seguida de una letra mayúscula que representa el término predicado.
| Símbolo | Proposición | Definición |
|---|---|---|
| SaP | Todo S es P | (x,Sx->Px)&(3x,Sx) |
| SeP | Ningún S es P | x,Sx->~Px |
| SiP | Algún S es P | 3x,Sx&Px |
| SoP | No todo S es P | (3x,Sx&~Px)|(~3x,Sx) |
| SuP | O bien Todo S es P o Ningún S es P | (x,Sx->Px)|(x,Sx->~Px) |
| SyP | Algún S es P y Algún S no es P | (3x,Sx&Px)&(3x,Sx&~Px) |
Para hacer que el tradicional Cuadro de oposición sea verdadero, las proposiciones de tipo A se definen con significado existencial y las proposiciones de tipo O se definen sin significado existencial, siguiendo los argumentos de Terence Parsons. También reconoce la forma de U y la forma de Y del Hexágono de Oposición.
Cualquiera de los términos en una proposición se pueden negar agregando el símbolo "~" por ejemplo, "~Aa~B" se interpretará como "todo no A es no B". Un "~" al principio de la expresión se adjunta al primer término y no a la expresión completa, por lo que "~Aa~B" no se interpreta como "~(Aa~B)" sino como "(~Aa~B)".
Aserciones numéricas
El lenguaje incluye un medio para hacer algunas afirmaciones simples de número. Los agregué al idioma solo por conveniencia; a veces ayudan a codificar la lógica en ciertos acertijos lógicos. No pertenecen a ninguna lógica simbólica que yo sepa.
Un número entero no negativo n seguido de una sola letra mayúscula P es una afirmación de que exactamente n objetos tienen la propiedad P .
Un número entero no negativo n seguido de más de una letra mayúscula P, Q, … es una afirmación de que exactamente n de las proposiciones P, Q, … son verdaderas.
| Ejemplo | Significación |
|---|---|
| 0P | Ningún objeto es P |
| 1P | Exactamente 1 objeto es P |
| 2P | Exactamente 2 objetos son P |
| 0PQR | Ninguna de P, Q y R son ciertas |
| 1PQR | Solo uno de P, Q y R es cierta |
| 2PQR | Exactamente 2 de P, Q y R son ciertas |
Reemplazos de texto
Una línea que comienza con "#replace" se interpretará como una directiva para reemplazar una cadena de letras o símbolos con otra en las líneas debajo de la directiva. Es una forma de definir sus propios símbolos de operador o dar nombres significativos a predicados y variables. Por ejemplo, cuando se le da el texto
#replace => -> #replace hombre H #replace mortal M #replace socrates s #replace porlotanto .'. x, hombre x => mortal x hombre socrates porlotanto mortal socrates
la aplicación lo convertirá en
x, H x -> M x M s .'. M s
antes de analizarlo sintácticamente.
El símbolo "Por lo tanto"
El símbolo "por lo tanto", ".'." (punto, apóstrofe, punto) se puede utilizar para probar argumentos lógicos. Se evaluará de la misma manera que el material condicional, pero el resultado mostrado será diferente. En lugar de indicar si el argumento es necesariamente cierto, contingente o imposible, el software indicará si el argumento es válido (necesariamente cierto) o inválido (no necesariamente cierto). Además, si el argumento es válido, el software indicará si las premisas son inconsistentes o la conclusión es tautológica.
Expresiones válidas
En este idioma, una expresión válida es solo una declaración de verdadero/falso. Puede ser una sola línea, como
P&Q->R
o pueden ser varias líneas, como
Hx->Mx Hs -> Ms
Si es una sola línea, el software interpreta la línea como una afirmación y decide si es válida, consistente o contradictoria. Si son varias líneas, el software une estas líneas para formar una sola expresión y decide esta declaración. El software trata cada línea que es una declaración como si estuviera unida a las otras líneas que son declaraciones con un AND lógico. Esto le permite distribuir una declaración larga en varias líneas. Por ejemplo,
P->Q Q->R P
se interpreta que significa lo mismo que
(P->Q)&(Q->R)&P
Si una expresión tiene varias líneas y exactamente una de ellas es un solo operador lógico binario o el símbolo "por lo tanto", el software unirá las líneas antes del operador con un "y" lógico, unirá las líneas después del operador con un "y" lógico y luego une estos dos conjuntos con el único operador lógico. Por ejemplo,
Hx->Mx Hs -> Ms
se interpreta que significa lo mismo que
( (Hx->Mx) & Hs ) -> (Ms)
Esto le permite expresar un argumento lógico (varias premisas seguidas de una conclusión) de una manera familiar, o probar si un conjunto de declaraciones es equivalente a otro conjunto de declaraciones sin ponerlas todas en una sola línea.
Las declaraciones largas se pueden dividir en varias líneas. El software interpretará el texto en varias líneas como una declaración de acuerdo con las siguientes reglas:
- Si una línea comienza entre paréntesis de apertura y cierre, se unirá con la línea anterior.
- Si una línea termina con un operador binario, se unirá a la línea siguiente.
- Si una línea comienza con un operador binario, se unirá con la línea anterior.
x,Ax|Bx|Cx
x,Ax |Bx |Cx
x,Ax| Bx| Cx
(x, Ax|Bx|Cx)
Por ejemplo, los siguientes bloques de texto se interpretan todos de la misma manera:
El espacio en blanco
Los tabuladores, los espacios y las líneas vacías siempre se ignoran. Podrías escribir esto:
((A |B|C)->J )<=>x,F x& y,Ix
o esto:
( (A | B |C )->J)<=> x ,Fx&y,I x
y esperar el mismo resultado. Los espacios en blanco se pueden utilizar para facilitar la lectura de las expresiones. Pero probablemente querría escribir esto en su lugar:
((A|B|C) -> J ) <=> x, Fx & y,Ix
porque es más fácil de leer.
Comentarios
El software ignora un "//" y todo lo que le sigue en una línea. Esto le permite agregar comentarios útiles a las expresiones, como
Hx->Mx // Todos los humanos son mortales. Hs // Sócrates es humano. .'. // Por lo tanto, Ms // Sócrates es mortal.
Criterios para el diseño del lenguaje
El lenguaje que utiliza esta aplicación es una especie de lógica simbólica. Fue diseñado con estos criterios en mente:
- El idioma solo debe usar caracteres ASCII básicos que están disponibles en un teclado estándar en inglés, por lo que es fácil para un usuario escribir expresiones.
- Las construcciones del lenguaje deben estar hechas de pocos caracteres para que puedan escribirse rápidamente.
- El lenguaje debe permitir que una persona organice la declaración de tal manera que sea fácil de leer.
- Los símbolos definidos en el idioma deben tener un precedente en otros idiomas. Los símbolos de este lenguaje se toman prestados de la lógica simbólica convencional, la notación matemática convencional y el lenguaje de programación C.
El algoritmo
Cuando el software decide una proposición, no opera sobre sentencias simbólicas. Opera en una estructura de datos similar a un árbol que la estructura lógica de la proposición. En este "árbol", cada nodo es un elemento de la proposición (un predicado, una variable, un cuantificador, etc.) y cada arista es una dependencia entre un elemento y sus elementos subordinados (por ejemplo, un AND lógico es un nodo con bordes que apuntan a los dos elementos a cada lado de la misma).
Analizando sintácticamente
El primer paso que toma el software es leer el texto que se le da e intentar convertirlo en un "árbol". Si tiene éxito, el texto es una declaración bien formada dentro del lenguaje simbólico del software y el software puede decidir el árbol. Hay más de una forma en que se puede realizar este análisis, por lo que los detalles no son importantes, siempre que el árbol resultante sea correcto.
La elección exacta del idioma tampoco es importante para el proceso de decisión. Siempre que un lenguaje solo represente elementos lógicos que son compatibles con el software y el lenguaje no permita que ningún elemento lógico dependa de sí mismo, directa o indirectamente (por ejemplo, sin la Paradojas de Mentiroso), este lenguaje podría reemplazar el lenguaje reconocido por este. el software y el algoritmo de decisión funcionarían de la misma manera.
Para algunos elementos que se pueden definir en términos de otros elementos, el software realiza sustituciones:
| Elemento | Reemplazo | |
|---|---|---|
| 3x,... | cuantificador existencial | (~x,~...) |
| 1x,... | descripción definitiva | (3y,x, x=y <=> ...) |
| <>... | posibilidad | (~[]~...) |
| ...^... | disyunción exclusiva | ~(...<=>...) |
Podría ser útil mostrar algunas declaraciones simbólicas y cómo se ven sus árboles correspondientes. Para la declaración w,Xw->Tw, que podría interpretarse como "todos mis ex viven en Texas", el software crea un árbol como este:
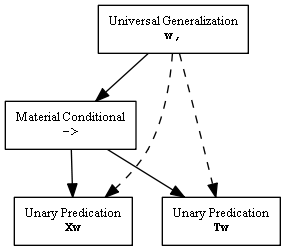
Los elementos de la declaración están todos aquí: una generalización universal, una implicación material debajo de ella y dos predicaciones debajo de esto. El conjunto declara una relación lógica entre ser ex de George Strait y vivir en Texas.
Las declaraciones más complicadas tienen árboles más complicados. Para el silogismo
Hx->Mx // Todos los humanos son mortales. Hs // Sócrates es humano. .'. // Por lo tanto, Ms // Sócrates es mortal.
el software crea este árbol:
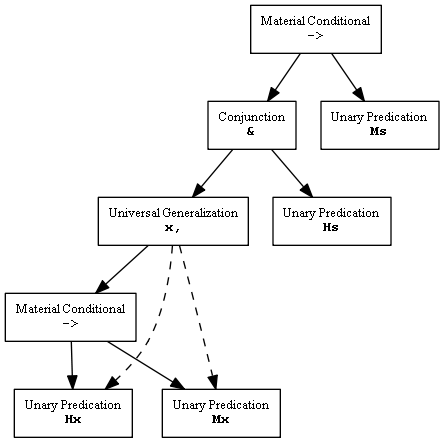
El argumento se ha convertido en una sola proposición; el software decidirá si el argumento es válido o no al decidir si esta proposición es cierta necesariamente o no.
Decisión
El software opera en árboles como los descritos anteriormente. Para decidir una proposición, para cada tipo de mundo, y a veces para cada tipo de mundo en cada interpretación, el software determina si la proposición representada por el árbol es cierta o equivocada. Si se encuentra que es cierta en cada tipo de mundo, se decide que es necesaria. Si se encuentra que es equivocada en cada tipo de mundo, se decide que es imposible. Si se encuentra que es cierta en algún tipo de mundo y equivocada en otro, se decide que es contingente. El software funciona de arriba hacia abajo. Cada nodo en el árbol es evaluado por evaluando sus nodos subordinados; ellos a su vez son evaluados por evaluando sus nodos subordinados. El procedimiento para evaluar un nodo depende de qué tipo de elemento lógico representa; cada elemento lógico tiene su propio procedimiento. Las siguientes secciones definen los procedimientos seguidos para cada elemento lógico.
Si la proposición no contiene ninguna modalidad o constante individual, la proposición se decide evaluando el árbol para cada tipo de mundo. Esto prueba efectivamente la proposición en todos los mundos posibles y, por lo tanto, es suficiente para decidir si la proposición es necesariamente verdadera, contingente o imposible.
Si la proposición contiene constantes individuales, la proposición se decide decidiendo otras dos proposiciones. La primera proposición se forma ligando todas las constantes individuales de la proposición original con generalizaciones universales. Si esta proposición es cierta, entonces la proposición original es necesariamente cierta. La segunda proposición se forma vinculando todas las constantes de la proposición original con cuantificadores existenciales. Si esta proposición es imposible, entonces la proposición original es imposible. En todos los demás casos, la proposición original es contingente.
Si la proposición contiene modalidades (posibilidad, necesidad), la proposición no puede decidirse simplemente evaluándola por todo tipo de mundo. Si se hiciera esto, tendría el efecto de tratar cada predicado nulo como si fuera una proposición contingente, y cada tipo de objeto como un tipo de objeto contingente. Tendría el efecto de hacer que el software decidiera modalidades de manera inesperada. Por ejemplo, el software decidiría que []P->~P es necesariamente cierto, ya que aquí se asumiría P ser siempre una proposición contingente y, por lo tanto, nunca necesariamente cierta. En cambio, el software evalúa la proposición bajo cada interpretación. Si es cierta para todo tipo de mundo bajo cada interpretación, entonces la proposición es necesariamente cierta.
Evaluación de una generalización universal
La manera obvia de evaluar una generalización universal es instanciar su variable con cada objeto en el mundo y evaluar cada uno de los proposiciones resultantes; si todas las instanciación son ciertas, la generalización es cierta; si alguna es falsa, la generalización es falsa. El problema con este enfoque es que un mundo puede tener una cantidad infinita de objetos, por lo que la evaluación en una cantidad de tiempo finita puede no ser posible. El software no intenta hacer esto. Se necesita un enfoque diferente, pero similar.
Supongamos que todos los objetos de un mundo se pueden agrupar en un número finito de tipos. Supongamos además que estos tipos se definen de tal manera que, si se instancia una generalización universal con cualquier objeto de un tipo, la proposición resultante es lógicamente equivalente a la proposición que resultaría de una instanciación con cualquier otro objeto del mismo tipo. Si todo esto es cierto, entonces la universalización es decidible. Y todo esto es cierto. Los elementos lógicos admitidos por el software permiten que los mundos posibles se agrupen de esta manera (la forma en que se realiza esta agrupación se define en otro lugar). Para evaluar una generalización universal, el software instancia la generalización universal con cada tipo de objeto hasta que se hayan probado todos los tipos de objetos o hasta que se encuentre que una instancia es falsa. Si todas las instancias son ciertas, la generalización universal es cierta, si alguna instancia es falsa, la generalización universal es falsa.
Evaluación de una conjunción ("y" lógico)
Para evaluar una conjunción, el software evalúa las proposiciones conjuntas. Si ambos son ciertas, la conjunción es cierta. Si alguna es falsa, la conjunción es falsa.)
Evaluación de una disyunción ("o" lógico)
Para evaluar una disyunción, el software evalúa las proposiciones separadas. Si ambas son falsas, la disyunción es falsa. Si una o otra de las dos es cierta, la disyunción es cierta.
Evaluación de una negación ("no" lógico)
Para evaluar una negación, el software evalúa la proposición negada. Si es cierta, la negación es falsa. Si es falsa, la negación es cierta.
Evaluación de un condicional material
Para evaluar un condicional material, el software evalúa su antecedente y su consecuente. Si el antecedente es cierta y el consecuente falso, entonces el condicional material es falso. En todos los demás casos, el condicional material es cierta.
Evaluación de una equivalencia
Para evaluar una equivalencia, el software evalúa ambos lados de la equivalencia. Si tienen el mismo valor de verdad, la equivalencia es cierta. Si tienen diferentes valores de verdad, la equivalencia es falsa.
Evaluación de una negación conjunta
Para evaluar una denegación conjunta, el software evalúa las proposiciones denegadas. Si ambas son falsas, la negación conjunta es cierta. Si cualquiera de las dos es cierta, la negación conjunta es falsa.
Evaluación de otros elementos lógicos
El software reemplaza todos los demás elementos lógicos admitidos por el lenguaje con combinaciones equivalentes de elementos, por lo que no necesita procesos adicionales para evaluarlos.
Evaluación de una necesidad
Si una proposición es necesariamente cierta, se determina evaluando la proposición en cada tipo de mundo que es posible bajo la interpretación de los predicados en la proposición. Si es cierta para todos estos tipos de mundos, entonces es necesariamente cierta. Si es falsa en tal tipo de mundo, no es necesariamente cierta. Prueba: Si la proposición es cierta en todos los tipos de mundos, entonces es cierta en todos los mundos posibles, y por lo tanto necesariamente cierta. Si la proposición es falsa en cualquier tipo de mundo, entonces es falsa en algún mundo posible, y por lo tanto no necesariamente cierta.
Evaluación de una predicación sobre una variable
Cada vez que el software evalúa una predicación unaria, ya ha instanciado la variable de la predicación con un tipo de objeto u otro. Prueba: dado que el software rechaza las proposiciones con variables no ligadas y define todas las cuantificaciones en términos de generalizaciones universales, si se evalúa una proposición, todas las variables de esta proposición están ligadas por generalizaciones universales. Dado que el software procede desde la parte superior del árbol hacia abajo, una predicación sobre una variable solo se evalúa para evaluar la generalización universal más arriba en el árbol que liga esta variable. Debido al proceso de evaluación de generalizaciones universales, el software siempre ha instanciado esta variable en el momento en que se evalúa la predicación.
La predicación es cierta si el predicado es cierto del tipo de objeto instanciado, y falsa si el predicado no es cierto para este tipo de objeto.
Evaluación de una predicación sin variables (un predicado nulo)
El tipo de mundo en cual el software evalúa actualmente el predicado nulo determina si este predicado nulo es cierto o falso. El tipo de mundo depende de la necesidad más cercana por encima de la predicación en el árbol. Si no hay necesidad por encima de la predicación, el tipo de mundo se elige como parte del proceso general de decisión.
Evaluación de una identificación
Cada vez que el software evalúa una identificación, ya ha instanciado cada una de las variables de la identificación con un tipo de objeto u otro. Prueba: dado que el software rechaza las proposiciones con variables no ligadas y define todas las cuantificaciones en términos de generalizaciones universales, si se evalúa una proposición, todas las variables de esta proposición están ligadas por generalizaciones universales. Dado que el software procede de la parte superior del árbol hacia abajo, la identificación de dos variables solo se evalúa para evaluar las generalizaciones universales más arriba en el árbol que unen estas variables. Debido al proceso de evaluación de generalizaciones universales, el software siempre ha instanciado estas variables en el momento en que se evalúa la predicación.
La identificación es cierta si sus variables han sido instanciadas con el mismo tipo de objeto, y falsa si han sido instanciadas con dos tipos de objetos diferentes. El software asume que la identidad transmundial de los indiscernibles es imposible; siempre considera que dos objetos son tipos diferentes de objetos si son de dos tipos diferentes de mundos. aquí.
Definiciones
Evaluar
Cuando el software evalúa una proposición, determina si es cierta o falsa según la interpretación actual, tipo del mundo, e instanciación de variables.
Decidir
Cuando el software decide una proposición, determina si es necesariamente cierta (válida), contingente (satisfacible pero no válida) o imposible (no satisfacible).
Modalidad
Una proposición gobernada por un operador modal. El software es compatible con las modalidades aleticas de posibilidad y necesidad.
Predicado unario
Un predicado unario es un predicado sobre una variable; el término "predicado monádico" es sinónimo, pero he elegido usar el término "predicado unario" por tres razones:
- En la mayoría de los lenguajes de programación, los operadores que tienen un operando (por ejemplo, negación, inversión de bits) se denominan "operadores unarios".
- En la programación funcional, especialmente en el lenguaje Haskell, "monádico" es un término significativo que se relaciona con las mónadas de la teoría de categorías y no predicar sobre una variable.
- Las palabras "unario" y "predicado" tienen sus raíces en latín. La palabra "monádico" tiene sus raíces en griego. Entonces, llamarlo "predicado monádico" mezcla raíces lingüísticas, pero llamarlo "predicado unario" no.
Un predicado unario es casi lo mismo que una propiedad. En este documento, los dos se usan indistintamente, excepto que un predicado unario "es cierta por" un objeto o "no es cierta por" un objeto, mientras que un objeto "tiene" o "no tiene" una propiedad.
Puede ser importante tener en cuenta que "predicado" y "predicación" son dos cosas diferentes. Un predicado es una proposición, propiedad o relación; una predicación es la aplicación de un predicado a unas variables.
Predicado nulo
Los predicados nulos son los mismos que las "proposiciones" en cálculo proposicional; son simplemente ciertas o falsas dentro de un mundo posible. Se pueden considerar como predicados sobre cero variables, predicados sobre nada, o sobre todo, dependiendo de cómo se mire. De ahí el término "predicado nulo".
Proposición
En este documento, la palabra "proposición" se usa de tres maneras diferentes, una para significar un predicado nulo, otra para significar cualquier idea que debe ser cierta o equivocada, y otra para significa una estructura de datos construida por el software que captura parte del contenido lógico de la idea que se supone que representa.
Mundo posible
El término elegido por los filósofos para denotar cualquier forma en que el universo podría ser, o podría haber sido, si no hubiera sido lo que es.
Tipos de mundos
Para decidir una proposición o evaluar una modalidad, todos los mundos posibles deben agruparse en un número finito de clases de mundos. Los siguientes párrafos describen cómo se hace esto.
Un predicado nulo es cierto o falso en un mundo posible. Una proposición de primer orden tiene solo un número finito de predicados nulos, por lo que con respecto a los predicados nulos en una proposición, los mundos posibles se pueden agrupar en tipos según cuáles de estos predicados nulos son verdaderos dentro de un mundo y cuáles son falsos. Para una proposición que contiene predicados nulos y ningún otro tipo de predicados, hay tantos tipos de mundos como combinaciones de predicados nulos que se pueden seleccionar de los predicados nulos en la proposición. Si una proposición contiene n predicados nulos, entonces hay 2n tipos de mundos para evaluar.
O un mundo tiene un tipo de objeto especifico o no lo tiene. Si una proposición contiene predicados unarios e identificaciones en el mundo pero no predicados nulos, los tipos de mundos que puede distinguir se definen en términos de los tipos de objetos presentes o ausentes en un mundo. Si el software define o tipos de objetos para tal proposición, entonces define 2o-1 tipos de mundos para esa proposición. Uno se resta del número total de combinaciones porque el mundo vacío se excluye de la evaluación. El software efectivamente asume que no existe tal cosa como un mundo vacío. Si no fuera así, el software decidiría que x,Ax&~Ax es posible. Tal vez debería.
Si una proposición contiene predicados nulos y predicados unarios o identificaciones dentro de un mundo, el software debe definir un tipo de mundo para cada combinación de predicados nulos verificados y combinaciones de tipos de objetos presentes. Este es solo el producto cartesiano de los dos, por lo que hay hasta 2n(2o-1 ) tipos de mundos que deben ser evaluados.
Una proposición que contiene modalidades podría involucrar identificaciones transmundiales, es decir, podría involucrar identificaciones cuyos sujetos podrían pertenecer a dos mundos que posible son diferentes. Por ejemplo, en "x,P&<>(3y,y=x & ~P)", y está dentro de una modalidad (<>) de la que x está fuera y, por lo tanto, x y y pueden pertenecer a mundos posibles que son diferentes cuando se evalúa y=x. Por ello, el software debe definir múltiples versiones de cada uno de los tipos de mundos mencionados en el párrafo anterior. Cuando hay t tales identificaciones transmundiales, hay hasta 2n(2o - 1) × t tipos de mundos que deben ser evaluados.
Tipos de objetos
Para evaluar una generalización universal, todos los objetos del mundo deben agruparse en un número finito de tipos de objetos. Los siguientes párrafos describen cómo se hace esto.
Si una proposición no contiene relaciones (por ejemplo, identificaciones, predicados binarios) y contiene un número finito de propiedades, no puede distinguir entre un objeto y otro si ambos objetos tienen las mismas propiedades. Por ejemplo, Xw->Tw es falso si w se instancia con cualquiera de un número ilimitado de objetos que no tienen la propiedad T pero tienen la propiedad X, independientemente de qué otras propiedades puedan tener estos objetos. Entonces, para tal proposición, los objetos se pueden agrupar en tipos según los predicados unarios de la proposición que verifican y falsifican. Habrá 2u de estas clases, una por cada combinación de predicados unarios que se pueda elegir entre u predicados unarios.
Si una proposición contiene identificaciones, agrupar objetos por tipos es más complicado. Dos objetos en una proposición pueden tener las mismas propiedades que se mencionan en la proposición y, sin embargo, no ser idénticos, por lo que no es suficiente definir clases solo por propiedades. Para las identificaciones, se supone que es suficiente evaluar cada combinación de 0 a i de cada combinación de predicados, donde i es el número máximo de variables libres distintas involucradas en las identificaciones para cualquier matriz ligada por un cuantificador dentro de la proposición. No tengo pruebas para esta suposición, pero parece funcionar.
En total, si hay u predicados unarios en una proposición y i es el máximo mencionado anteriormente, se deben evaluar hasta i2u tipos de objetos.
Interpretaciones
Al decidir una proposición que no contiene ninguna modalidad, el software define tantos tipos de mundos como sea posible bajo las suposiciones de que
- Todos los predicados nulos son contingentes y no tienen necesariamente ninguna relación lógica entre sí.
- Todas las combinaciones de propiedades son posibles. Por ejemplo, 3x,Px&Qx siempre es posible, por lo tanto no pueden interpretar P y Q como "rojo" y "no rojo", respectivamente.
Esto funciona para proposiciones que no contienen modalidades, pero no funcionará para proposiciones que contienen modalidades. Para proposiciones que contienen modalidades, el software debe evaluar la proposición con estos supuestos, pero también debe evaluar la proposición con cualquier otro conjunto de supuestos que es posible sobre las relaciones de los predicados nulos entre sí y con los tipos de objetos en un mundo. El software hace esto definiendo interpretaciones. Una interpretación es un conjunto de tipos de mundos; contiene todo tipo de mundo que es posible bajo una interpretación dada de los predicados en la proposición, y ningún otro tipo de mundo. Para evaluar una proposición con todas las interpretaciones posibles, el software simplemente evalúa la proposición con cada subconjunto no vacío de los tipos de mundos que define para la proposición. Entonces, si hay tipos de mundos u para una proposición, entonces hay 2u-1 interpretaciones que deben evaluarse.
Notas
Semántica de la lógica modal cuantificada
Identidad transmundial
Parece común en las discusiones sobre la lógica modal cuantificada suponer que dos objetos en dos mundos posibles diferentes pueden ser idénticos de alguna manera; se consideran el mismo objeto. En todas las lógicas modales cuantificadas que he encontrado, el operador de igualdad ("=") significa este tipo de identidad. Desarrollé el manejo de este software de la lógica modal cuantificada sin saber que este tipo de identidad era lo que normalmente se usaba en la lógica modal cuantificada y, en consecuencia, hice que "=" indicara el único tipo de identidad que sabía estaba bien definida: identidad de indiscernibles. Esto causa el modal cuantificado del software ser inusual, pero espero que no sea inútil. Es posible representar la identidad común en el lenguaje del software. Considere lo que significa que dos objetos en dos mundos diferentes sean el mismo objeto. Si digo "Si no me hubiera sentido tan mal el lunes, habría ido a trabajar", estoy hablando de dos mundos posibles: el mundo real y un mundo contrafactual donde fui a trabajar el lunes, pero estoy hablando de una persona que existe en ambos mundos. Pero, ¿qué es lo que los hace iguales? Mi primera suposición sería que comparten una propiedad en común — el de ser yo — y cada uno de ellos es el único objeto en su respectivo mundo que tiene esa propiedad, pero no es tan simple. En algún otro mundo, George Washington podría no haber sido el primer presidente de los Estados Unidos de América. Si empezáramos a escribir una historia alternativa sobre los EE. UU. como hubiera sido si George Washington nunca hubiera sido presidente, probablemente consideraríamos que el George Washington que no es presidente es la misma persona que el George Washington real, pero no consideraríamos a quien sea. De lo contrario, elegimos ser el primer presidente para ser la misma persona que el primer presidente real de los EE. UU., aunque son los únicos poseedores de la propiedad de ser el primer presidente de los EE. UU. en sus respectivos mundos. ¿Por qué? Esta es una pregunta interesante, pero para los propósitos inmediatos de escribirla como una declaración simbólica, no necesita respuesta.
Para capturar esta noción de identidad que se usa habitualmente en la lógica modal en este lenguaje, elegiríamos un predicado para representar la propiedad que se supone que los dos objetos tienen en común, afirmaríamos que no más de un objeto en un mundo puede tener esa propiedad, y luego afirmar que ambos objetos tienen esta propiedad. Por ejemplo:
// En cualquier mundo, solo puede haber un primer presidente de los EE. UU. []x,y, Px&Py -> x=y // George Washington fue el primer presidente de los Estados Unidos. x,Gx -> Px // George Washington podría no haber sido el primer presidente de los Estados Unidos. <>3x,Gx&~Px
Desafortunadamente, el software no admite declaraciones de esta complejidad, y por lo tanto no puede decidir declaraciones que utilicen esta representación de identidad transmundial.
Instanciacións de objetos dentro de expresiones modales
Los cuantificadores siempre se evalúan dentro de un tipo de mundo. Solo se extienden sobre los objetos que existen en este tipo de mundo. No estoy seguro de si debería llamarlo "actualist", pero la idea es al menos similar a la idea en Mundos posibles. Entonces, cada vez que se crea una instancia de una variable con un tipo de objeto, se fija el tipo de mundo en el que existe. Esto implica que "x, Px -> []Px" es necesariamente cierto. Si quisiera expresar la proposición si algo es P, entonces necesariamente es P, podría usar la formulación de identidad transmundial descrita anteriormente:
// Elija R arbitrariamente. []x,y, Rx&Ry -> x=y // En cualquier mundo, no hay más de una R. x, Rx & (Px -> []y, Ry -> Py)
Desafortunadamente, esta expresión implica demasiadas interpretaciones y el software la rechazará.
Eficiencia y limitaciones del tiempo de ejecución
Como se puede ver al combinar las fórmulas dadas en las secciones sobre tipos de objetos, tipos de mundos y interpretaciones, para decidir una propuesta sin modalidades, el software debe evaluar la propuesta en hasta 2n × Max(0, 2i2u - 1) tipos de mundos, donde n es el número de predicados nulos distintos en la proposición, u es el número de predicados unarios distintos en la proposición, y i es el número máximo de variables libres distintas que son involucradas en identificaciones para cualquier matriz limitada por un cuantificador dentro de la proposición, o 1 si la proposición contiene variables pero no identificaciones, o 0 si la proposición no contiene variables. Para decidir una proposición con modalidades, el software debe evaluar la proposición en hasta 22n ;× Max(0, 2i2u - 1) interpretaciones. Esto significa que el algoritmo no escala bien; su tiempo de ejecución es exponencial o superexponencial en relación con la complejidad de la proposición que se decide. Sin embargo, esto no impide que el software funcione lo suficientemente rápido al decidir proposición con valores pequeños para n, u y i.
En realidad, el software define ī2u tipos de objetos, donde ī es i redondeado a la potencia de 2 más cercana. No es necesario que i se redondee para que el algoritmo sea correcto, pero facilita la codificación de tipos de objetos como números binarios. Además, para mantener la codificación binaria simple, define mundos vacíos, pero los omite al evaluar las proposiciones. El software en realidad codifica tipos de mundos e interpretaciones como números binarios de 32 bits. Esto permite que el software funcione rápido, pero pone un límite estricto a la complejidad de las propuestas que puede decidir; n + ī2u ≤ 32 para proposiciones no modales y 2n + ī2u ≤ 32 para proposiciones modales.
Las siguientes tablas enumeran los valores combinados más grandes de n, u y i que admite el software.
| 5 | 0 | 0 |
| 4 | 0 | 2 |
| 3 | 1 | 2 |
| 3 | 0 | 4 |
| 2 | 0 | 8 |
| 1 | 2 | 2 |
| 1 | 1 | 4 |
| 1 | 0 | 16 |
| 0 | 0 | 17 |
| 32 | 0 | 0 |
| 31 | 0 | 2 |
| 30 | 1 | 2 |
| 30 | 0 | 4 |
| 29 | 0 | 8 |
| 28 | 2 | 2 |
| 28 | 1 | 4 |
| 28 | 0 | 16 |
| 27 | 0 | 17 |
| 26 | 1 | 8 |
| 24 | 3 | 2 |
| 24 | 2 | 4 |
| 24 | 1 | 16 |
| 22 | 1 | 17 |
| 20 | 2 | 8 |
| 16 | 4 | 2 |
| 16 | 3 | 4 |
| 16 | 2 | 16 |
| 12 | 2 | 17 |
| 8 | 3 | 8 |
| 0 | 5 | 2 |
| 0 | 4 | 4 |
| 0 | 3 | 16 |
Contacto
Puede ponerse en contacto conmigo (el desarrollador de esta aplicación) enviándome un correo electrónico a g@sgnimuc.eiznekcammail.com o agregando un comentario a esta publicación de blog. Estoy dispuesto a responder preguntas o brindar ayuda sobre el uso del software.
Me harías un favor si me avisaras de
- errores en el software,
- decisiones incorrectas tomadas por el software, o
- declaraciones poco claras o equivocadas en este documento.
También,
- Si encuentra útil esta aplicación, me gustaría saber para qué la usa.
- Si hay alguna parte de la interfaz de usuario que encuentra confusa, dígame e intentaré mejorarla.
- Si tiene ideas para nuevas funciones, no dude en sugerirlas. Estoy abierto a expandir la funcionalidad de esta aplicación, siempre y cuando esté en consonancia con el enfoque basado en los mundos posibles que el software utiliza para decidir propuestas.
Gracias.